Desigualdades de concentración

This website hosts the materials for a minicourse on concentration inequalities that I taught at the National University of Colombia in November of 2023. The course was delivered in Spanish. If you are interested in this subject, I strongly recommend the free video lectures on High-Dimensional Probability by, the great, Roman Vershynin.

En este minicurso los asistentes tendrán la oportunidad de profundizar en el estudio de desigualdades de concentración clásicas y contemporáneas. A lo largo de tres sesiones, exploraremos desigualdades reconocidas, como las de Markov y Hoeffding, así como desigualdades más generales aplicables a variables aleatorias subgaussianas y subexponenciales. Además, se abordarán las versiones matriciales equivalentes de algunas de estas desigualdades. La teoría del curso será ilustrada con aplicaciones modernas, tales como el modelo de bloques estocásticos y reducción de dimensión, permitiendo así a los participantes adquirir habilidades aplicables en campos tan variados como la ciencia de datos, la teoría de redes y más. A través de una mezcla equilibrada de teoría y práctica, los estudiantes estarán preparados para utilizar estas poderosas herramientas en su trabajo e investigación futura, desarrollando un entendimiento sólido y aplicable de las desigualdades de concentración.

El curso está basado en el maravilloso libro de Roman Vershynin, “High-dimensional probability.” Pueden encontrar una copia gratuita aquí. Otras referencias muy buenas incluyen:

Boucheron, Stéphane, Gábor Lugosi, and Olivier Bousquet. Concentration Inequalities (2013).
Tropp, Joel A. Probability in High Dimensions. Lecture notes (Caltech) (Winter 2023).
Van Handel, Ramon. Probability in High Dimension. Lecture Notes (Princeton University) (2014).

Notas #

Ejercicios #

Estos ejercicios están pensados para complementar los conceptos que cubrimos en clase. No se calificarán o corregirán, por favor no me manden las soluciones!

Problema 1 #

Demuestre que para todo $x \in \mathbb{R}$ tenemos que $\cosh(x) \leq \exp{x^2}$.

Problema 2 #

Demuestre que la norma sub-gaussiana de una variable aleatoria $X$ acotada por $1$ está acotada por \[ \|X\|_{\psi_2} \leq \frac{1}{\sqrt{\log(2)}}. \]

Problema 3 #

Considere la siguiente versión de la desigualdad de Hoeffding.

Teorema. Sea $X_1, \ldots, X_n$ variables aleatorias independientes. Suponga que $X_i \in [m_i, M_i]$ para cada $i$. Entonces, para cualquier $t > 0$, tenemos \[ \mathbb{P}\left(\sum_{i=1}^{n} (X_i - \mathbb{E} X_i) \geq t\right) \leq \exp\left(-\frac{2t^2}{\sum_{i=1}^{N} (M_i - m_i)^2}\right). \]

Pruebe este resultado, posiblemente con alguna otra constante absoluta en lugar de 2 en la cola.

Problema 4 #

Sea $X$ una variable aleatoria con esperanza cero. Demuestre que $X$ es sub-gaussiana si y solo si exists una constant $K > 0$ tal que para todo $\lambda \in \mathbb{R}$, \[ \mathbb{E}\exp(\lambda X) \leq \exp(K^2 \lambda^2). \]

Problema 5 #

Sea $X$ una variable aleatoria sub-gaussiana. Defina \[ \|X\|_{\psi_2} = \inf\{K>0 \colon \mathbb{E}\exp(X^2/K^2) \leq 2\}. \] Demuestre que $\|\cdot\|_{\psi_2}$ es una norma en el espacio de variables aleatorias sub-gaussianas.

Problema 6 #

Sea $(\mathcal{T}, d)$ un espacio metrico y $K \subseteq \mathcal{T}$ un subconjunto. Fije un $\epsilon > 0$, demuestre la siquiente desigualdad \[ \mathcal{P}(K, d, 2\epsilon) \leq \mathcal{N}(K, d, \epsilon) \] donde $\mathcal{P}(K, d, \epsilon)$ y $\mathcal{N}(K, d, \epsilon)$ son el numero de empaquetamiento y de recubrimiento, respectivamente.

Problema 7 #

En nuestra definición de los números de cobertura de $K$, requerimos que los centros $ x_i $ de las bolas $ B(x_i, \varepsilon) $ que forman una cobertura estén en $K$. Relajando esta condición, defina el número de cobertura exterior $ N_{\text{ext}}(K, d, \varepsilon) $ de manera similar pero sin requerir que $ x_i \in K $. Demuestre que \[ N_{\text{ext}}(K, d, \varepsilon) \leq N(K, d, \varepsilon) \leq N_{\text{ext}}(K, d, \varepsilon/2). \]

Problema 8 #

Dé un contraejemplo a la siguiente propiedad de monotonicidad: \[ L \subset K \quad \text{implica} \quad N(L, d, \varepsilon) \leq N(K, d, \varepsilon). \] Demuestre una versión aproximada de monotonicidad: \[ L \subset K \quad \text{implica} \quad N(L, d, \varepsilon) \leq N(K, d, \varepsilon/2). \]

Problema 9 #

Sea $A ∈ \mathbb{R}^{n × m} y $ ε ∈ (0, 1/2)$. Entonces para cualquier par de $\epsilon$-mallas $\mathcal{N} \subseteq \mathbb{S}^{m-1}$ y $\mathcal{M} \subseteq \mathbb{S}^{n-1}$ tenemos que \[ \sup_{x \in \mathcal{N}, y \in \mathcal{M}} \langle y, Ax \rangle \leq \|A\| \leq \frac{1}{1-2\epsilon} \sup_{x \in \mathcal{N}, y \in \mathcal{M}} \langle y, Ax \rangle. \]

Problema 10 #

Recuerde el teorema de Davis-Kahan que vimos en clase:

Teorema. Sean $S$ y $T$ matrices simetricas $n \times n$. Fije un indice $i \in [n]$ tal que \[ \min_{j \colon j \neq i} |\lambda_i(S) - \lambda_j(S)| = \delta > 0. \] Entonces, \[ \sin \angle (v_i(S), v_i(T)) \leq \frac{2\|S - T\|}{\delta}, \] donde $v_i(X)$ es el $i$-esimo vector propio de $X$ y $\angle(u,v)$ denota el angulo entre $u$ y $v$ con valores entre $[0, \pi/2]$.

Demuestre que la conclusion del Teorema de Davis-Kahan que probamos en clase implica que existe $\theta \in \{-1, 1\}$ tal que \[ \|v_i(S) - \theta v_i(T)\|_2 \leq 2^{3/2}\frac{\|S - T\|}{\delta}. \]

Problema 11 #

Sea $A$ la matriz de adyacencia de un grafo aleatorio dado por el modelo de bloques estocastico $G(n, p, q)$ con $n$ par y $p > q$. Suponga que ordenamos los nodos del grafo de forma que \[D:= \mathbb{E}(A) = \begin{pmatrix} p \mathbf{J} & q \mathbf{J} \\ q \mathbf{J} & p\mathbf{J} \end{pmatrix}\] donde $\mathbf{J} \in \{1\}^{n/2 \times n/2}$ es la matriz de solo unos. Demuestre que esta matriz tiene rango dos y que sus valores propios y vectors propios son \[ \lambda_1 = \left(\frac{p+q}{2}\right) n ,\quad v_1 = \begin{pmatrix} 1 \\ \vdots \\ 1 \\ 1 \\ \vdots \\1 \end{pmatrix}, \quad \lambda_2 = \left(\frac{p-q}{2}\right) n, \quad \text{and} \quad v_2 = \begin{pmatrix} 1 \\ \vdots \\ 1 \\ -1 \\ \vdots \\ -1 \end{pmatrix}. \]

Problema 12 #

Sea $X \sim \text{Unif}(\mathbb{S}^{d-1})$. Demuestre que $\|\sqrt(d)X_1\|_{\psi_2} \leq C$ para alguna constante $C > 0$ independiente de la dimension.

Problema 13 #

Sea $X \sim \text{Unif}(\mathbb{S}^{d-1})$ y $f \colon \mathbb{S}^{d-1} \rightarrow \mathbb{R}$ sea una funcion $L$-Lipschitz. Demuestre que \[ \|f(X) - \mathbb{E }f(X)\|_{\psi_2} \leq C\frac{L}{\sqrt{d}} \] para alguna constante $C > 0$ independiente de la dimension.

Experimentos numericos #

Estos son los experimentos que vimos en clase como motivacion.

Modelo de bloques estocasticos: Deteccion de comunidades #

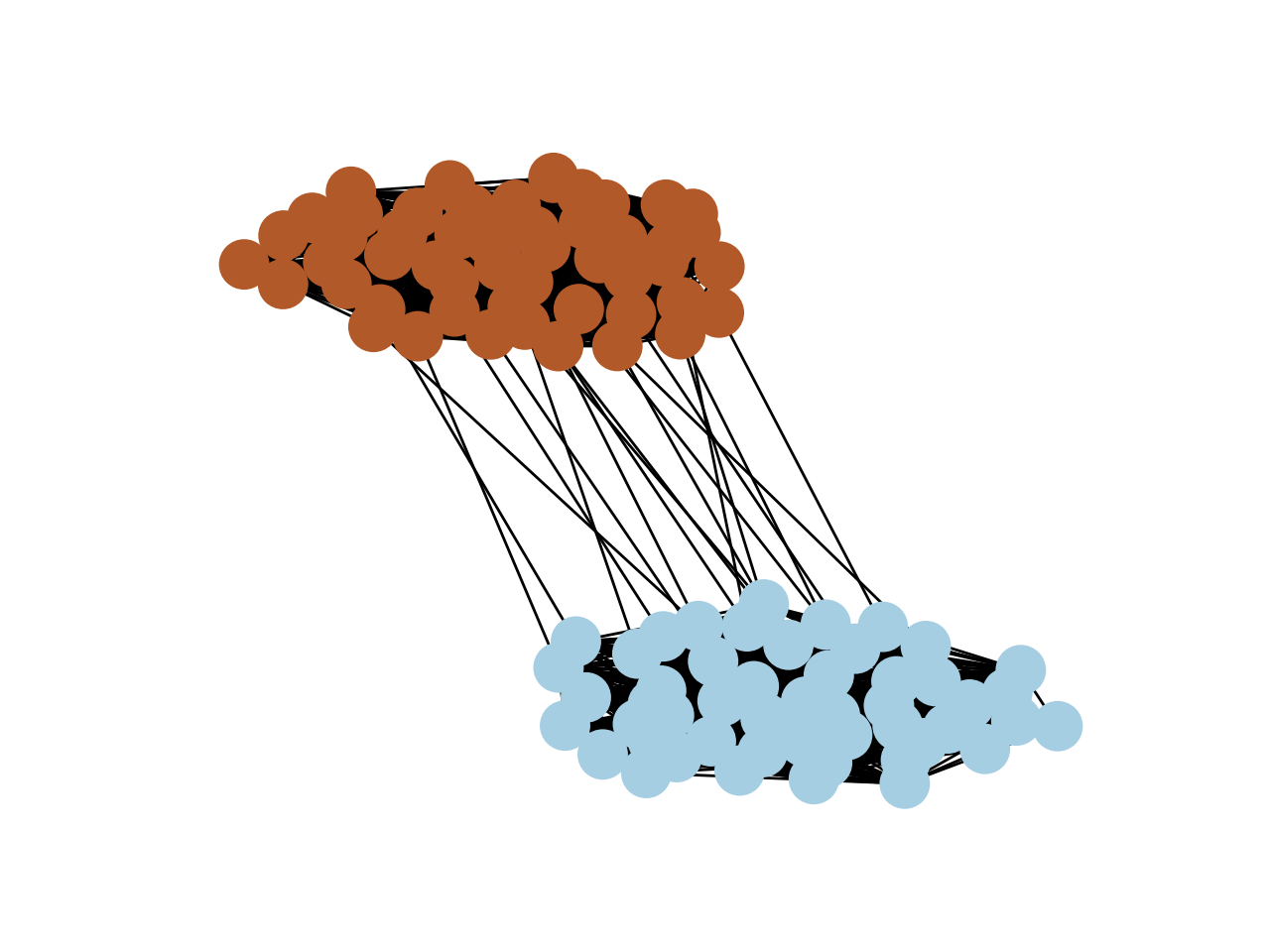
Primero generamos un grafo aleatorio y dibujamos las etiquetas reales.

import networkx as nx
import matplotlib.pyplot as plt
from matplotlib.backends.backend_agg import FigureCanvasAgg as FigureCanvas
import numpy as np
from scipy.linalg import eigh

# Generate a random Stochastic Block Model graph
n = 100
p = 0.7
q = 0.01
sizes = [n // 2, n - n // 2]
probs = [[p, q], [q, p]]
G = nx.stochastic_block_model(sizes, probs)

# Plot the graph with labels as colors
fig, ax = plt.subplots()
pos = nx.spring_layout(G)
labels = [G.nodes[v]['block'] for v in G.nodes()]
nx.draw(G, pos, node_color=labels, cmap=plt.cm.Paired, ax=ax)
canvas = FigureCanvas(fig)
filename = "true_labels.png"
canvas.print_figure(filename)
plt.close(fig)
filename

Ahora corremos el metodo espectral para estimar las etiquetas.

# Compute the second eigenvector of the adjacency matrix
A = nx.adjacency_matrix(G).toarray()
w, v = eigh(A)
fiedler_vector = v[:, -2]

# Use the signs of the Fiedler vector as labels
estimated_labels = np.sign(fiedler_vector)

# Plot the graph with estimated labels
fig2, ax2 = plt.subplots()
nx.draw(G, pos, node_color=estimated_labels, cmap=plt.cm.Paired, ax=ax2)
canvas2 = FigureCanvas(fig2)
filename2 = "estimated_labels.png"
canvas2.print_figure(filename2)
plt.close(fig2)
filename2

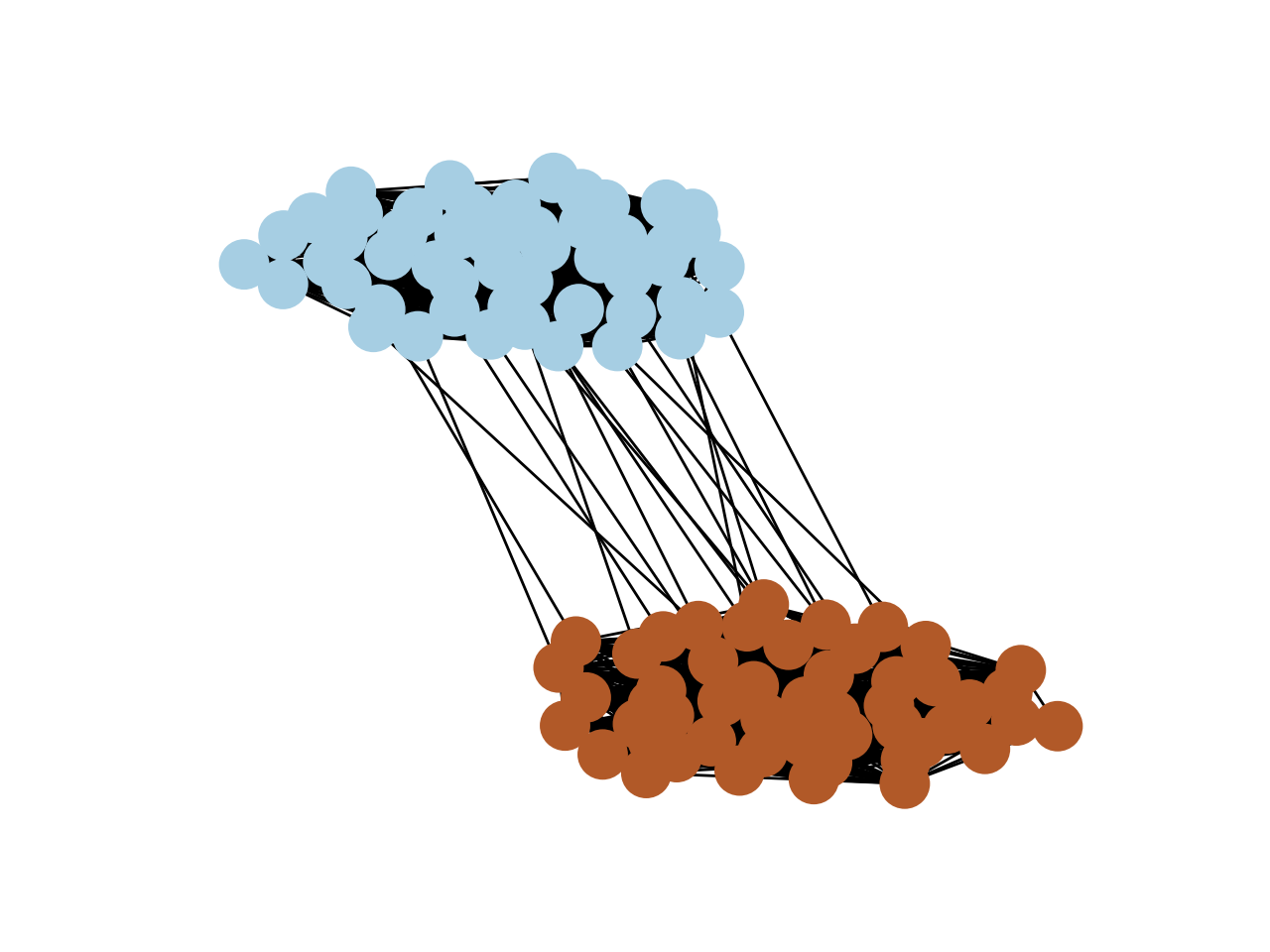
Finalmente, midamos el error.

true_labels = np.array([1 if G.nodes[v]['block'] == 0 else -1 for v in G.nodes()])
error = min(np.sum(true_labels != estimated_labels),
            np.sum(true_labels != -estimated_labels))
print("Misclassification error (up to sign):", error)
f'El error de clasificacion es {error}'

El error de clasificacion es 0

Johnson-Lindenstrauss: Reduccion de dimension #

import numpy as np
import matplotlib.pyplot as plt

def random_orthogonal_projection(n, m):
    G = np.random.randn(n, m)
    Q, R = np.linalg.qr(G)
    return Q[:, :m]

def random_projection(X, m):
    d = X.shape[1]
    P = random_orthogonal_projection(d, m)
    return np.sqrt(d / m) * X.dot(P)

def norm_distortion(original, projected):
    original_norm = np.linalg.norm(original, axis=1)
    projected_norm = np.linalg.norm(projected, axis=1)
    distortion =  np.abs(original_norm - projected_norm) / original_norm
    return np.max(distortion)

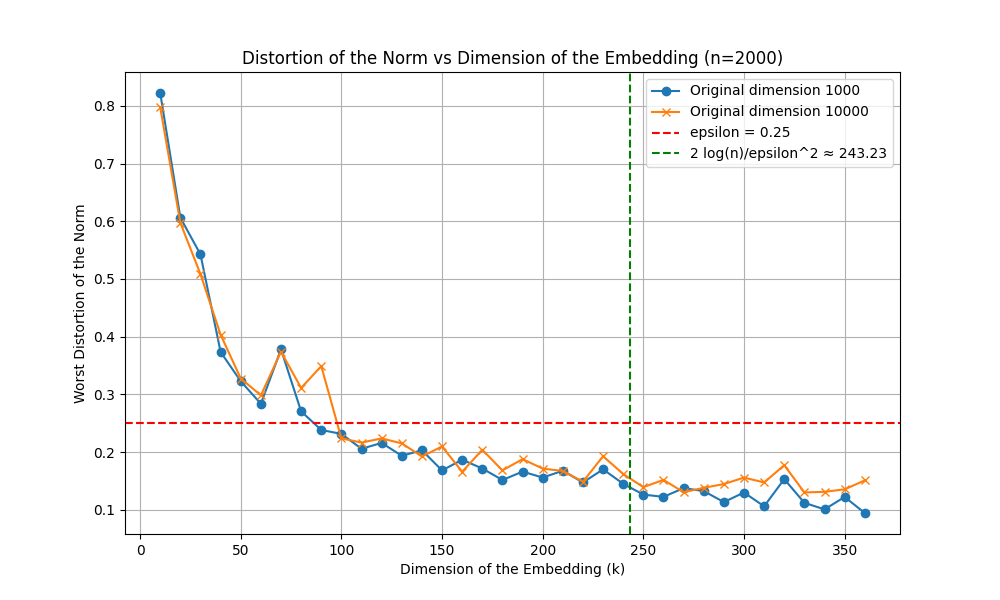
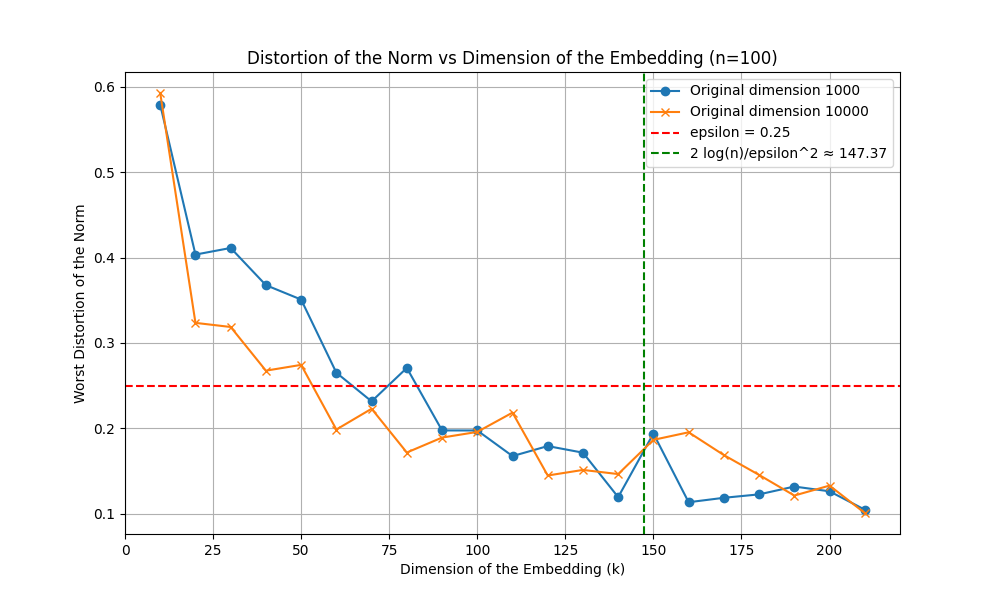
def run_experiment(n, eps):
    d, D = 1000, 10000
    k_values = np.arange(10, 3*int(np.log(n)/eps**2), 10)
    X_d = np.random.randn(n, d)
    X_D = np.random.randn(n, D)

    distortions_d = [norm_distortion(X_d, random_projection(X_d, k)) for k in k_values]
    distortions_D = [norm_distortion(X_D, random_projection(X_D, k)) for k in k_values]

    theoretical_k = 2 * np.log(n) / eps**2

    plt.figure(figsize=(10, 6))
    plt.plot(k_values, distortions_d, marker='o', label=f"Original dimension {d}")
    plt.plot(k_values, distortions_D, marker='x', label=f"Original dimension {D}")
    plt.axhline(eps, color='r', linestyle='--', label=f'epsilon = {eps}')
    plt.axvline(theoretical_k, color='g', linestyle='--', label=f'2 log(n)/epsilon^2 ≈ {theoretical_k:.2f}')
    plt.title(f'Distortion of the Norm vs Dimension of the Embedding (n={n})')
    plt.xlabel('Dimension of the Embedding (k)')
    plt.ylabel('Worst Distortion of the Norm')
    plt.legend()
    plt.grid(True)

    image_file = f'jl-lemma-plot-n-{n}.png'
    plt.savefig(image_file)
    plt.close()
    return image_file

# Plot for n = 100
image_file_100 = run_experiment(100, 0.25)
image_file_100

Ahora con mas puntos.

image_file_2000 = run_experiment(2000, 0.25)
image_file_2000